已知抛物线y=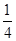 x2-4与x轴交于A,B两点(点A在点B的左侧).顶点为点C.
x2-4与x轴交于A,B两点(点A在点B的左侧).顶点为点C.
(1)求直线AC的解析式;
(2)试问在抛物线的对称轴上是否存在一个定点,使得过该定点的任意一条直线与抛物线有两个交点时,这两个交点与抛物线顶点的连线互相垂直?并说明理由.
相关知识点
推荐套卷
已知抛物线y=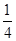 x2-4与x轴交于A,B两点(点A在点B的左侧).顶点为点C.
x2-4与x轴交于A,B两点(点A在点B的左侧).顶点为点C.
(1)求直线AC的解析式;
(2)试问在抛物线的对称轴上是否存在一个定点,使得过该定点的任意一条直线与抛物线有两个交点时,这两个交点与抛物线顶点的连线互相垂直?并说明理由.