如图1,矩形纸片ABCD的边长AB=4cm,AD=2cm.同学小明现将该矩形纸片沿EF折痕,使点A与点C重合,折痕后在其一面着色(如图2),观察图形对比前后变化,回答下列问题:

(1)GF FD:(直接填写=、>、<)
(2)判断△CEF的形状,并说明理由;
(3)小明通过此操作有以下两个结论:
①四边形EBCF的面积为4cm2
②整个着色部分的面积为5.5cm2
运用所学知识,请论证小明的结论是否正确.
相关知识点
推荐套卷
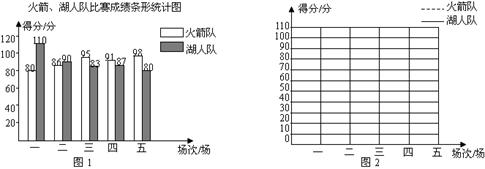
 ,请你计算湖人队五场比赛成绩的平均得分
,请你计算湖人队五场比赛成绩的平均得分 ;
;


 粤公网安备 44130202000953号
粤公网安备 44130202000953号