二次函数y=x2-2mx+3(m>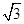 )的图象与x轴交于点A(a,0)和点B(a+n,0)(n>0且n为整数),与y轴交于C点.
)的图象与x轴交于点A(a,0)和点B(a+n,0)(n>0且n为整数),与y轴交于C点.
(1)若a=1,①求二次函数关系式;②求△ABC的面积;
(2)求证:a=m- ;
;
(3)线段AB(包括A、B)上有且只有三个点的横坐标是整数,求a的值.
相关知识点
推荐套卷
二次函数y=x2-2mx+3(m>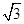 )的图象与x轴交于点A(a,0)和点B(a+n,0)(n>0且n为整数),与y轴交于C点.
)的图象与x轴交于点A(a,0)和点B(a+n,0)(n>0且n为整数),与y轴交于C点.
(1)若a=1,①求二次函数关系式;②求△ABC的面积;
(2)求证:a=m- ;
;
(3)线段AB(包括A、B)上有且只有三个点的横坐标是整数,求a的值.