（本题9分）如图(1)，在直角梯形OABC中，BC∥OA，∠OCB＝90°，OA＝6，AB＝5，cos∠OAB＝
．
(1)写出顶点A、B、C的坐标；
(2)如图(2)，点P为AB边上的动点（P与A、B不重合），PM⊥OA，PN⊥OC，垂足分别为M，N．设PM＝x，四边形OMPN的面积为y．
①求出y与x之间的函数关系式，并写出自变量x的取值范围；
②是否存在一点P，使得四边形OMPN的面积恰好等于梯形OABC的面积的一半？如果存在，求出点P的坐标；如果不存在，说明理由．
相关试题
、（本题8分）如图，CD为⊙O的直径，点A在⊙O上，过点A作⊙O的切线交CD的延长线于点F。已知∠F＝30°。
（1）求∠C的度数；
⑵若点B在⊙O上，AB⊥CD，垂足为E，AB＝
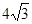，求图中阴影部分的面积.
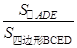的值
的值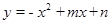
经过点A (1,0), B(O，-6). 
的图象与一次函数
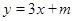的图象相交于点（1，5）。
轴，交直线BC于点F，求线段DF的长，并求△BCD的面积；相关知识点
推荐套卷
粤公网安备 44130202000953号