(本小题满分8分)从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组 ,第二组
,第二组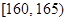 ,……,第八组
,……,第八组 ,得到频率分布直方图如右.
,得到频率分布直方图如右.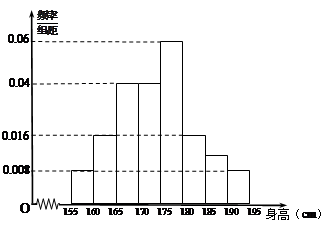
(Ⅰ)计算第七组[185,190)的样本数;并估计这个高一年级800名学生中身高在170厘米以下的人数;
(Ⅱ) 求出这100名学生身高的中位数、平均数.
相关知识点
推荐套卷
(本小题满分8分)从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组 ,第二组
,第二组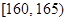 ,……,第八组
,……,第八组 ,得到频率分布直方图如右.
,得到频率分布直方图如右.
(Ⅰ)计算第七组[185,190)的样本数;并估计这个高一年级800名学生中身高在170厘米以下的人数;
(Ⅱ) 求出这100名学生身高的中位数、平均数.