(本小题满分12分)为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下:

(1)用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图,根据散点图判断: 与y=
与y=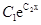 哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)
哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)

其中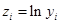 ;
;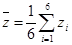
(2)根据(1)的判断最佳结果及表中的数据,建立y关于x 的回归方程。
参考公式: 

推荐套卷
(本小题满分12分)为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下:

(1)用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图,根据散点图判断: 与y=
与y=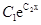 哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)
哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)

其中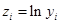 ;
;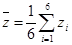
(2)根据(1)的判断最佳结果及表中的数据,建立y关于x 的回归方程。
参考公式: 
