已知:二次函数y=ax2+bx+6(a≠0)与x轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.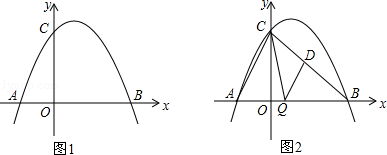
(1)请直接写出点A、B的坐标,并求出该二次函数的解析式.
(2)如图1,在二次函数对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
相关知识点
推荐套卷

 的值.
的值.
 =1.414,
=1.414, =1.732,
=1.732, =2.449)
=2.449)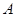 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与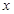 轴相交于点
轴相交于点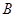 ,连结
,连结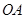 ,抛物线y=x
,抛物线y=x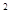
 从点
从点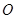 沿
沿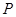 ,顶点
,顶点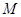 到
到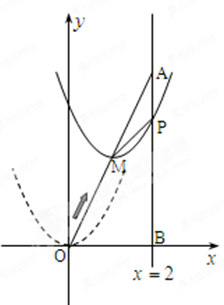
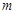 ,
,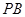 最短;
最短;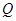 ,使△
,使△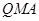 的面积与△
的面积与△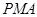 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点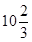 m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
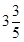 ,问:此次跳水会不会失误?通过计算说明理由.
,问:此次跳水会不会失误?通过计算说明理由.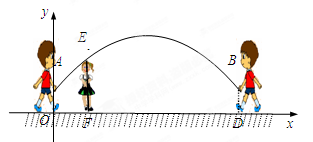
 粤公网安备 44130202000953号
粤公网安备 44130202000953号