如图,在平面直角坐标系中,已知点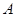
坐标为（2,4）,直线x=2与
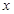轴相交于点
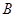,连结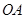
,抛物线y=x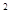
从点
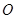沿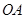方向平移,与直线x=2交于点
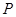,顶点
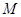到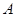点时停止移动．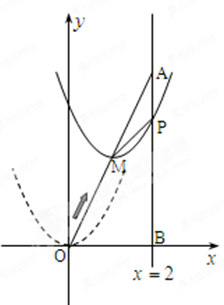
（1）求线段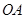所在直线的函数解析式;
（2）设抛物线顶点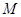的横坐标为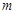
,
①用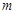的代数式表示点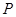的坐标;
②当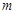为何值时,线段
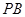最短;
（3）当线段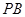最短时,相应的抛物线上是否存在点
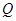,使△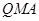
的面积与△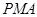
的面积相等,若存在,请求出点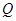的坐标;若不存在,请说明理由．
相关试题
你能化简(x－1)(x99＋x98＋x97＋……＋x＋1）吗？遇到这样的问题，我们可以先思考一下，从简单的情形入手．
分别计算下列各式的值：
①(x－1)(x＋1）＝x2－1；
②(x－1)(x2＋x＋1）＝x3－1；；
③(x－1)(x3＋x2＋1）＝x4－1；；……
由此我们可以得到：(x－1）(x99＋x98＋x97＋…＋x＋1）＝________________；
请你利用上面的结论，完成下面两题的计算：
(1) 299＋298＋297＋……＋2＋1；
(2)(－2)50＋(－2)49＋(－2)48＋……＋（－2）＋1
.如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点.
（1）画出△ABC的AB边上的中线CD；
（2）画出△ABC向右平移4个单位后得到的△A1B1C1；
（3）图中AC与A1C1的关系是：_____________.
（4）图中△ABC的面积是_______________.
(3)
相关知识点
推荐套卷
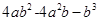
粤公网安备 44130202000953号