(本小题满分12分)学校生活区内建有一块矩形休闲区域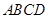 ,
, ,
, ,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路
,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路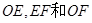 ,考虑到学校整体规划,要求
,考虑到学校整体规划,要求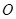 是
是 的中点,点
的中点,点 在边
在边 上,点
上,点 在边
在边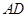 上,且
上,且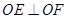 如图所示.
如图所示.
(1)设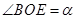 ,试将
,试将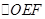 的周长
的周长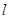 表示成
表示成 的函数关系式,并求出此函数的定义域;
的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为800元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
推荐套卷
(本小题满分12分)学校生活区内建有一块矩形休闲区域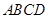 ,
, ,
, ,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路
,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路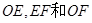 ,考虑到学校整体规划,要求
,考虑到学校整体规划,要求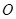 是
是 的中点,点
的中点,点 在边
在边 上,点
上,点 在边
在边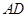 上,且
上,且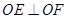 如图所示.
如图所示.
(1)设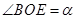 ,试将
,试将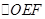 的周长
的周长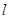 表示成
表示成 的函数关系式,并求出此函数的定义域;
的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为800元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.