用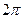
平方米的材料制成一个有盖的圆锥形容器，如果在制作过程中材料无损耗，且材料的厚度忽略不计，底面半径长为
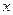，圆锥母线的长为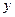
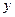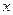（1）、建立与的函数关系式，并写出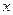的取值范围；
（2）、圆锥的母线与底面所成的角大小为
，求所制作的圆锥形容器容积多少立方米(精确到0. 01m3)
．（1）求B的大小； （2）若
，
，求b．
的最小正周期
求
的值
为正常数，且
的通项公式；
恒成立？若存在，求出相应的M的最小值；若不存在，请说明理由。相关知识点
推荐套卷
用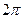平方米的材料制成一个有盖的圆锥形容器，如果在制作过程中材料无损耗，且材料的厚度忽略不计，底面半径长为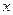，圆锥母线的长为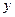
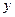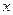（1）、建立与的函数关系式，并写出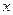的取值范围；
（2）、圆锥的母线与底面所成的角大小为，求所制作的圆锥形容器容积多少立方米(精确到0. 01m3)
粤公网安备 44130202000953号