某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
相关知识点
推荐套卷
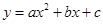 (
(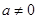 )的对称轴为直线
)的对称轴为直线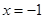 ,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.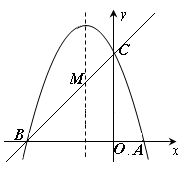
 经过B、C两点,求直线BC和抛物线的解析式;
经过B、C两点,求直线BC和抛物线的解析式;
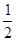 BC.
BC.
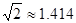 ,
,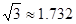 )
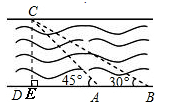
)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号