阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)= (x>0)是减函数.
(x>0)是减函数.
证明:假设x1<x2,且x1>0,x2>0
f(x1)﹣f(x2)= ﹣
﹣ =
= =
=
∵x1<x2,且x1>0,x2>0
∴x2﹣x1>0,x1x2>0
∴ >0,即f(x1)﹣f(x2)>0
>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)= (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
(1)函数f(x)= (x>0),f(1)=
(x>0),f(1)= =1,f(2)=
=1,f(2)= =
= .
.
计算:f(3)= ,f(4)= ,猜想f(x)= (x>0)是 函数(填“增”或“减”);
(x>0)是 函数(填“增”或“减”);
(2)请仿照材料中的例题证明你的猜想.
相关知识点
推荐套卷
 .
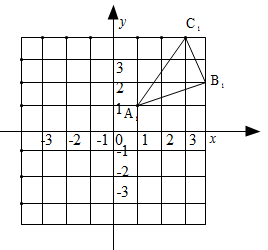
. 内,正方形AOBC顶点C的坐标为(2,2),过点B的直线∥OC,P是直线上一个动点,抛物线
内,正方形AOBC顶点C的坐标为(2,2),过点B的直线∥OC,P是直线上一个动点,抛物线 过O、C、P三点.
过O、C、P三点.
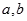 的关系式是 .
的关系式是 .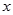 的取值范围 .
的取值范围 . 粤公网安备 44130202000953号
粤公网安备 44130202000953号