某日，小敏、小君两人约好去奥体中心打球．小敏13：00从家出发，匀速骑自行车前往奥体中心，小君13：05从离奥体中心6000m的家中匀速骑自行车出发．已知小君骑车的速度是小敏骑车速度的1．5倍．设小敏出发x min后，到达离奥体中心y m的地方，图中线段AB表示y与x之间的函数关系．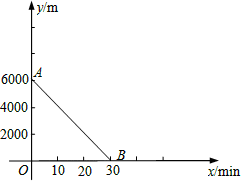
（1）小敏家离奥体中心的距离为 m；她骑自行车的速度为 m/min；
（2）求线段AB所在直线的函数表达式；
（3）小敏与小君谁先到奥体中心，要等另一人多久？
相关试题
综合与实践
主题：制作无盖正方体形纸盒．
素材：一张正方形纸板．
步骤1：如图1，将正方形纸板的边长三等分，画出九个相同的小正方形，并剪去四个角上的小正方形；
步骤2：如图2，把剪好的纸板折成无盖正方体形纸盒．
猜想与证明：（1）直接写出纸板上 与纸盒上 的大小关系；
（2）证明（1）中你发现的结论．
2023年5月30日，神舟十六号载人飞船发射取得圆满成功，3名航天员顺利进驻中国空间站．如图中的照片展示了中国空间站上机械臂的一种工作状态．当两臂 ，两臂夹角 时，求 两点间的距离．（结果精确到 ，参考数据： ）
相关知识点
推荐套卷
粤公网安备 44130202000953号