“你今天光盘了吗?”这是国家倡导厉行节约,反对浪费以来的时尚流行语,某校团委随机抽取部分了学生,对他们是否了解关于“光盘行动”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.团委根据调查的数据进行整理,绘制了尚不完整的统计图如下,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题:
(1)求本次活动共调查了多少名学生?
(2)请补全图2,并求出图1中,B区域的圆心角度数;
(3)若该校有2400名学生,请估算该校不是了解很多的学生人数.
相关知识点
推荐套卷
 .如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,过C作直线交DE于A,交DF于B.若DB=
.如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,过C作直线交DE于A,交DF于B.若DB= ,求DA的长度.
,求DA的长度.
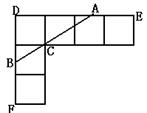

 这样的线段,并选择其中的一个说明这样画的道理.
这样的线段,并选择其中的一个说明这样画的道理.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号