武汉轻轨一号线开通后学生上学大为便捷.为了了解学生上学所用的交通工具的乘坐情况,在全校学生中进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题:
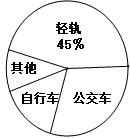
(1)此次共调查了 名同学;
(2)将条形图补充完整,并计算扇形统计图中公交车部分的圆心角的度数;
(3)如果全校共有1000名学生,估计该校乘坐轻轨上学的学生有 人.
相关知识点
推荐套卷
武汉轻轨一号线开通后学生上学大为便捷.为了了解学生上学所用的交通工具的乘坐情况,在全校学生中进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题:
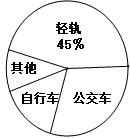
(1)此次共调查了 名同学;
(2)将条形图补充完整,并计算扇形统计图中公交车部分的圆心角的度数;
(3)如果全校共有1000名学生,估计该校乘坐轻轨上学的学生有 人.