【问题提出】
如图①,已知⊿ABC是等边三角形,点E在线段AB上,点D在直线BC上,且DE=EC,将⊿BCE绕点C顺时针旋转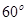 至⊿ACF,连接EF.
至⊿ACF,连接EF.
试证明:AB=DB+AF.
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其它条件不变,线段AB、DB、AF之间又有怎样的数量关系?请说明理由.
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间数量关系,不必说明理由.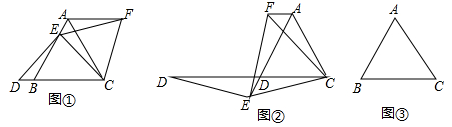
相关知识点
推荐套卷
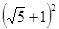
 ,求作:线段MN, 使其同时满足下列3个条件(要求:用尺规作图,保留作图痕迹,不写作法和结论):
,求作:线段MN, 使其同时满足下列3个条件(要求:用尺规作图,保留作图痕迹,不写作法和结论):
 为直角,点
为直角,点 为线段
为线段 的中点,点
的中点,点 是射线
是射线 上的一个动点(不与点
上的一个动点(不与点 重合),连结
重合),连结 ,作
,作 ,垂足为
,垂足为 ,连结
,连结 ,过点
,过点 ,交
,交 于
于 .
. 取什么值或范围时,有AC//EF,并说明理由。
取什么值或范围时,有AC//EF,并说明理由。

 粤公网安备 44130202000953号
粤公网安备 44130202000953号