(本题10分)2014年我区正在推进的旅游产业中,对外宣传的优秀景点有:A:溱湖湿地公园;B:姜堰生态园;C:溱潼老街;D:北大街古文化区;E:“全球500佳”河横.区旅游管理部门对某月进入景点的人数情况调查统计,制成了两幅不完整的统计图(如图).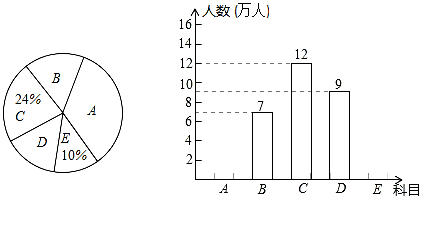
(1)求出这个月进入我区上述五个景点的总人数;
(2)请你补全频数分布直方图;
(3)求出扇统计图中A,溱湖湿地公园所对应的扇的圆心角的度数.
相关知识点
推荐套卷
(本题10分)2014年我区正在推进的旅游产业中,对外宣传的优秀景点有:A:溱湖湿地公园;B:姜堰生态园;C:溱潼老街;D:北大街古文化区;E:“全球500佳”河横.区旅游管理部门对某月进入景点的人数情况调查统计,制成了两幅不完整的统计图(如图).
(1)求出这个月进入我区上述五个景点的总人数;
(2)请你补全频数分布直方图;
(3)求出扇统计图中A,溱湖湿地公园所对应的扇的圆心角的度数.