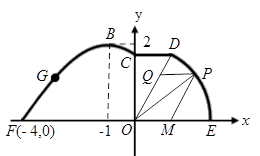
(本小题12分)如图,在海岸线 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段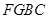 ,该曲线段是函数
,该曲线段是函数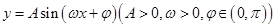 ,
,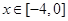 的图像,图像的最高点为
的图像,图像的最高点为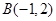 .边界的中间部分为长
.边界的中间部分为长 千米的直线段
千米的直线段 ,且
,且 .游乐场的后一部分边界是以
.游乐场的后一部分边界是以 为圆心的一段圆弧
为圆心的一段圆弧 .
.
(1)求曲线段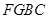 的函数表达式;
的函数表达式;
(2)曲线段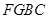 上的入口
上的入口 距海岸线
距海岸线 最近距离为
最近距离为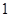 千米,现准备从入口
千米,现准备从入口 修一条笔直的景观路到
修一条笔直的景观路到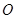 ,求景观路
,求景观路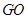 长;
长;
(3)如图,在扇形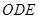 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区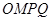 ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线 上,一边在半径
上,一边在半径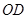 上,另外一个顶点
上,另外一个顶点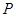 在圆弧
在圆弧 上,且
上,且 ,求平行四边形休闲区
,求平行四边形休闲区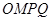 面积的最大值及此时
面积的最大值及此时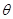 的值.
的值.
推荐套卷
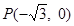 作直线
作直线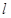 与椭圆
与椭圆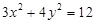 相交于
相交于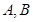 两点,
两点,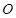 为坐标原点,求
为坐标原点,求 面积的最大值及此时直线倾斜角的正切值。
面积的最大值及此时直线倾斜角的正切值。 的顶点
的顶点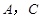 在椭圆
在椭圆 上,对角线
上,对角线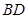 所在直线的斜率为1.
所在直线的斜率为1.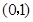 时,求直线
时,求直线 的方程;
的方程; 时,求菱形
时,求菱形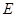 中心在原点
中心在原点 ,焦点在
,焦点在 轴上,其离心率
轴上,其离心率 ,过点
,过点 的直线
的直线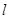 与椭圆
与椭圆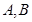 两点,且C分有向线段
两点,且C分有向线段 的比为2.
的比为2.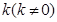 表示
表示 的面积;
的面积; :
: 及点
及点
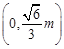 ,在⊙
,在⊙
 与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若
与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若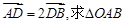 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号