（1）已知：如图1，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．
（2）如图2，AB切⊙O于点B，OA=2，∠OAB=30°，弦BC∥OA．求：劣弧BC的长．（结果保留π）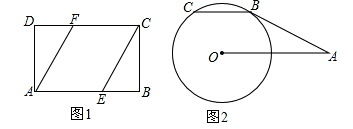
+
·
）÷
;推荐套卷
（1）已知：如图1，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．
（2）如图2，AB切⊙O于点B，OA=2，∠OAB=30°，弦BC∥OA．求：劣弧BC的长．（结果保留π）
粤公网安备 44130202000953号