给定数列 ,如果存在常数
,如果存在常数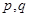 使得
使得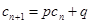 对任意
对任意 都成立,则称
都成立,则称 为“M类数列”
为“M类数列”
(1)若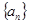 是公差为
是公差为 的等差数列,判断
的等差数列,判断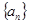 是否为“M类数列”,并说明理由;
是否为“M类数列”,并说明理由;
(1)若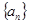 是“M类数列”且满足:
是“M类数列”且满足: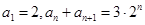
①求 及
及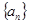 的通项公式;
的通项公式;
②设数列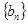 满足:对任意的正整数
满足:对任意的正整数 ,都有
,都有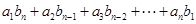
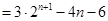 ,且集合
,且集合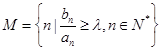 中有且仅有3个元素,试求实数
中有且仅有3个元素,试求实数 的取值范围.
的取值范围.
相关知识点
推荐套卷
给定数列 ,如果存在常数
,如果存在常数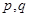 使得
使得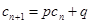 对任意
对任意 都成立,则称
都成立,则称 为“M类数列”
为“M类数列”
(1)若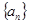 是公差为
是公差为 的等差数列,判断
的等差数列,判断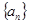 是否为“M类数列”,并说明理由;
是否为“M类数列”,并说明理由;
(1)若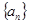 是“M类数列”且满足:
是“M类数列”且满足: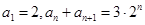
①求 及
及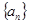 的通项公式;
的通项公式;
②设数列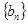 满足:对任意的正整数
满足:对任意的正整数 ,都有
,都有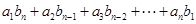
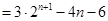 ,且集合
,且集合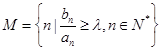 中有且仅有3个元素,试求实数
中有且仅有3个元素,试求实数 的取值范围.
的取值范围.