如图,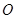 是坐标原点,过点
是坐标原点,过点 的抛物线
的抛物线 与
与 轴的另一个交点为
轴的另一个交点为 ,与
,与 轴交于点
轴交于点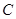 ,其顶点为
,其顶点为 点.
点.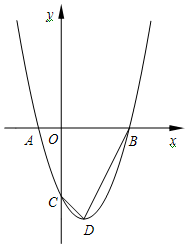
(1)求 的值.
的值.
(2)连结 、
、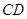 ,动点
,动点 的坐标为
的坐标为 .
.
①当四边形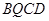 是平行四边形时,求
是平行四边形时,求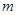 的值;
的值;
②连结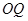 、
、 ,当
,当 最大时,求出点
最大时,求出点 的坐标.
的坐标.
推荐套卷
如图,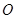 是坐标原点,过点
是坐标原点,过点 的抛物线
的抛物线 与
与 轴的另一个交点为
轴的另一个交点为 ,与
,与 轴交于点
轴交于点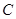 ,其顶点为
,其顶点为 点.
点.
(1)求 的值.
的值.
(2)连结 、
、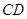 ,动点
,动点 的坐标为
的坐标为 .
.
①当四边形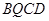 是平行四边形时,求
是平行四边形时,求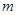 的值;
的值;
②连结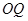 、
、 ,当
,当 最大时,求出点
最大时,求出点 的坐标.
的坐标.