阅读理解：
如图①，如果四边形ABCD满足AB=AD，CB=CD，∠B=∠D=90°，那么我们把这样的四边形叫做“完美筝形”．
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状，再展开得到图③，其中CE，CF为折痕，∠BCE=∠ECF=∠FCD，点B′为点B的对应点，点D′为点D的对应点，连接EB′，FD′相交于点O．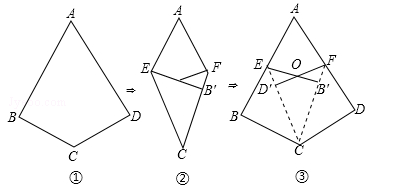

简单应用：
（1）在平行四边形、矩形、菱形、正方形四种图形中，一定为“完美筝形”的是         ；
（2）当图③中的∠BCD=120°时，∠AEB′=       °；
（3）当图②中的四边形AECF为菱形时，对应图③中的“完美筝形”有     个（包含四边形ABCD）．
拓展提升：
（4）当图③中的∠BCD=90°时，连接AB′，请探求∠AB′E的度数，并说明理由．