（本题5分）“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的函数图象刻画了“龟兔再次赛跑”的故事（x表示乌龟从起点出发所行的时间，y1表示乌龟所行的路程，y2表示兔子所行的路程）．有下列说法：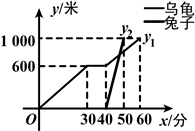
①“龟兔再次赛跑”的路程为1000米；
②兔子和乌龟同时从起点出发；
③乌龟在途中休息了10分钟；
④兔子比乌龟先到达终点．
其中正确的说法是________．（把你认为正确说法的序号都填上）
相关试题
如图1，在平面直角坐标系中，抛物线与 轴分别交于 、 两点，与 轴交于点 ，抛物线的顶点坐标为 ，连结 、 、 ．
（1）求抛物线的表达式；
（2）判断 的形状，并说明理由；
（3）如图2，以 为圆心， 为半径作 ，在 上是否存在点 ，使得 的值最小，若存在，请求出最小值；若不存在，请说明理由．
如图1， 为 上一点，点 在直径 的延长线上，且 ．
（1）判断直线 与 的位置关系，并说明理由；
（2）若 ， ，求 的半径；
（3）如图2，在（2）的条件下， 的平分线 交 于点 ，交 于点 ，连结 ．求 的值．
如图，一次函数 的图象与反比例函数 的图象交于点 、 ，与 轴交于点 ，若 ，且 ．
（1）求反比例函数与一次函数的表达式；
（2）请直接写出不等式 的解集．
粤公网安备 44130202000953号