如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年
年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:
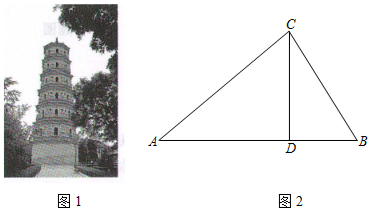
方案设计:如图2,宝塔
垂直于地面,在地面上选取
,
两处分别测得
和
的度数
,
,
在同一条直线上).
数据收集:通过实地测量:地面上
,
两点的距离为
,
,
.
问题解决:求宝塔
的高度(结果保留一位小数).
参考数据:
,
,
,
,
,
.
根据上述方案及数据,请你完成求解过程.