(本题6分)如图,已知RtΔABC中,∠C=90°,BC=4,AC=4,现将ΔABC沿CB方向平移到Δ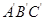 的位置,若平移距离为3.
的位置,若平移距离为3.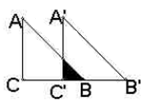
(1)求ΔABC与Δ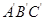 的重叠部分的面积;
的重叠部分的面积;
(2)若平移距离为x(0≤x≤4),求ΔABC与Δ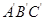 的重叠部分的面积y,则y与x有怎样的关系?
的重叠部分的面积y,则y与x有怎样的关系?
(本题6分)如图,已知RtΔABC中,∠C=90°,BC=4,AC=4,现将ΔABC沿CB方向平移到Δ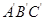 的位置,若平移距离为3.
的位置,若平移距离为3.
(1)求ΔABC与Δ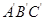 的重叠部分的面积;
的重叠部分的面积;
(2)若平移距离为x(0≤x≤4),求ΔABC与Δ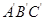 的重叠部分的面积y,则y与x有怎样的关系?
的重叠部分的面积y,则y与x有怎样的关系?