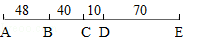一条单线铁路线上有A，B，C，D，E五个车站，它们之间的路程如下图所示（单位：千米）．两列火车从A，E相向对开，A车先开了3分钟，每小时行60千米，E车每小时行50千米，两车在车站上才能停车，互相让道、错车．两车应该安排在哪一个车站会车（相遇），才能使停车等候的时间最短，先到的火车至少要停车多长时间？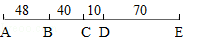
相关试题
如图，已知△ABC的三个顶点分别为A（2，3）、B（3，1）、C（－2，－2）。
（1）请在图中画出△ABC关于y轴的轴对称图形△DEF（A、B、C的对应点分别是D、E、F），并直写出D、E、F的坐标。
（2）求四边形ABED的面积。
；
，0）作直线
⊥x轴，点P在直线
粤公网安备 44130202000953号