（本小题满分16分）已知点
为椭圆
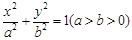上的任意一点（长轴的端点除外），
、
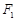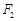分别为左、右焦点，其中a，b为常数．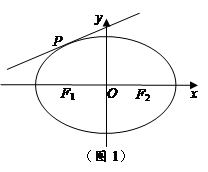
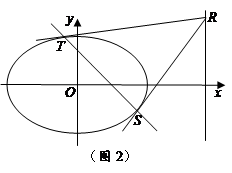
（1）若点P在椭圆的短轴端点位置时，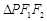
为直角三角形，求椭圆的离心率．
（2）求证：直线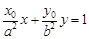
为椭圆在点P处的切线方程；
（3）过椭圆的右准线上任意一点R作椭圆的两条切线，切点分别为S、T．请判断直线ST是否经过定点？若经过定点，求出定点坐标，若不经过定点，请说明理由．
相关试题
数列
且
，
等比数列
且
，
，
分别是
的对称轴
前项和为
，且点
在
图像上，求
的三边长
满足
，
，求
的取值范围．推荐套卷
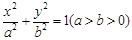（本小题满分16分）已知点为椭圆上的任意一点（长轴的端点除外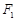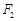），、分别为左、右焦点，其中a，b为常数．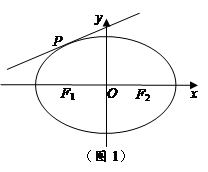
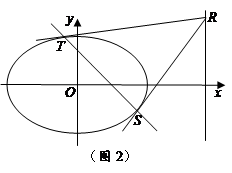
（1）若点P在椭圆的短轴端点位置时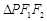，为直角三角形，求椭圆的离心率．
（2）求证：直线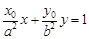为椭圆在点P处的切线方程；
（3）过椭圆的右准线上任意一点R作椭圆的两条切线，切点分别为S、T．请判断直线ST是否经过定点？若经过定点，求出定点坐标，若不经过定点，请说明理由．
粤公网安备 44130202000953号