(本小题满分14分)如图所示,直线 与x轴、y轴分别交于A、B两点,抛物线
与x轴、y轴分别交于A、B两点,抛物线 经过A、B两点,与x轴的另一个交点为C,连接BC.
经过A、B两点,与x轴的另一个交点为C,连接BC.
(1)求抛物线的解析式及点C的坐标;
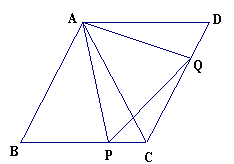
(2)点P从点C出发,沿线段CA由C向A运动,同时点Q从点B出发,沿线段BC由B向C运动,P、Q的运动速度都是每秒1个单位长度,当Q点到达C点时,P、Q同时停止运动,试问在坐标平面内是否存在点D,使P、Q运动过程中的某一时刻,以C、D、P、Q为顶点的四边形为菱形?若存在,求出点D的坐标;若不存在,说明理由.
相关知识点
推荐套卷
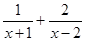 计算结果是
计算结果是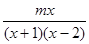 ,求常数m的值;
,求常数m的值;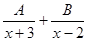 计算结果是
计算结果是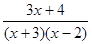 ,求常数A、B的值.
,求常数A、B的值.
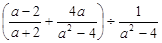 .其中a =-
.其中a =-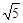 ”马小虎同学做题时把“a = -
”马小虎同学做题时把“a = - 粤公网安备 44130202000953号
粤公网安备 44130202000953号