(·吉林长春)如图,在等边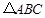 中,
中,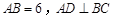 于点
于点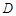 ,点
,点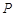 在边
在边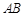 上运动,过点
上运动,过点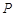 作
作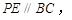 与边
与边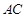 交于点
交于点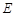 ,连结
,连结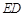 ,以
,以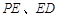 为邻边作□
为邻边作□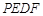 ,设□
,设□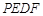 与
与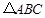 重叠部分图形的面积为
重叠部分图形的面积为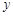 ,线段
,线段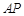 的长为
的长为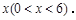
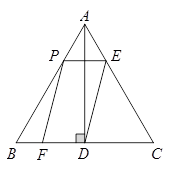
(1)求线段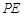 的长(用含
的长(用含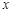 的代数式表示);
的代数式表示);
(2)当四边形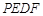 为菱形时,求
为菱形时,求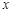 的值;
的值;
(3)求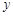 与
与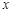 之间的函数关系式;
之间的函数关系式;
(4)设点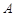 关于直线
关于直线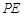 的对称点为点
的对称点为点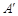 ,当线段
,当线段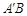 的垂直平分线与直线
的垂直平分线与直线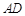 相交时,设其交点为
相交时,设其交点为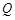 ,当点
,当点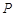 与点
与点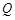 位于直线
位于直线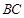 同侧(不包括点
同侧(不包括点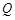 在直线
在直线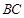 上)时,直接写出
上)时,直接写出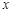 的取值范围.
的取值范围.
(·吉林长春)如图,在等边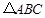 中,
中,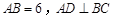 于点
于点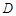 ,点
,点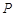 在边
在边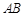 上运动,过点
上运动,过点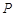 作
作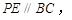 与边
与边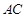 交于点
交于点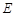 ,连结
,连结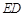 ,以
,以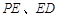 为邻边作□
为邻边作□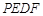 ,设□
,设□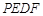 与
与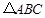 重叠部分图形的面积为
重叠部分图形的面积为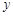 ,线段
,线段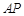 的长为
的长为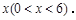
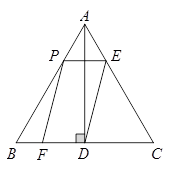
(1)求线段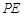 的长(用含
的长(用含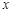 的代数式表示);
的代数式表示);
(2)当四边形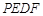 为菱形时,求
为菱形时,求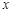 的值;
的值;
(3)求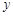 与
与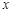 之间的函数关系式;
之间的函数关系式;
(4)设点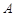 关于直线
关于直线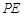 的对称点为点
的对称点为点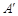 ,当线段
,当线段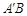 的垂直平分线与直线
的垂直平分线与直线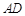 相交时,设其交点为
相交时,设其交点为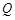 ,当点
,当点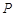 与点
与点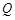 位于直线
位于直线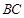 同侧(不包括点
同侧(不包括点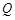 在直线
在直线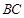 上)时,直接写出
上)时,直接写出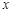 的取值范围.
的取值范围.