(本小题满分12分)为了分流地铁高峰的压力,市发改委通过听众会,决定实施低峰优惠票价制度.不超过 公里的地铁票价如下表:
公里的地铁票价如下表:
乘坐里程 (单位: (单位: ) ) |
 |
 |
 |
| 票价(单位:元) |
 |
 |
 |
现有甲、乙两位乘客,他们乘坐的里程都不超过 公里.已知甲、乙乘车不超过
公里.已知甲、乙乘车不超过 公里的概率分别为
公里的概率分别为 ,
, ,甲、乙乘车超过
,甲、乙乘车超过 公里且不超过
公里且不超过 公里的概率分别为
公里的概率分别为 ,
, .
.
(Ⅰ)求甲、乙两人所付乘车费用不相同的概率;
(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
相关知识点
推荐套卷
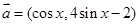 ,
, ,
,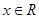 ,设函数
,设函数 .
. 的最大值;
的最大值; 中,角
中,角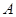 为锐角,角
为锐角,角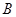 、
、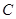 的对边分别为
的对边分别为 、
、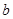 、
、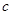 ,
,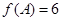 ,且
,且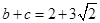 ,求
,求 ,且
,且 在
在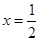 处的切线方程为
处的切线方程为 .
.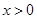 时,恒有
时,恒有 ;
; ,
, ,且
,且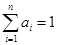 ,则
,则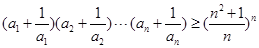 .
.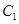 ,抛物线
,抛物线 的焦点均在
的焦点均在 轴上,
轴上,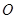 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:

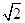


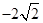

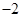
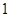
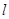 与
与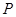 ,且与
,且与 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点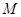 ,使得以
,使得以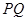 为直径的圆恒过点
为直径的圆恒过点 中,
中, ,
,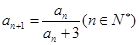 .
.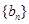 满足
满足 ,数列
,数列 项和为
项和为 ,若不等式
,若不等式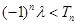 对一切
对一切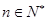 恒成立,求
恒成立,求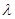 的取值范围.
的取值范围. 中,
中,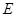 是
是 的中点,
的中点,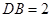 ,
,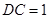 ,
, ,
,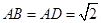 ,将左图沿直线
,将左图沿直线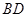 折起,使得二面角
折起,使得二面角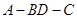 为
为 ,如右图.
,如右图.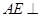 平面
平面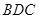 ;
; 与平面
与平面 所成角的余弦值.
所成角的余弦值.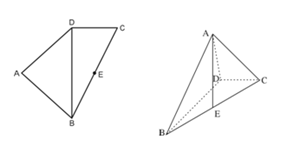
 粤公网安备 44130202000953号
粤公网安备 44130202000953号