如图1,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.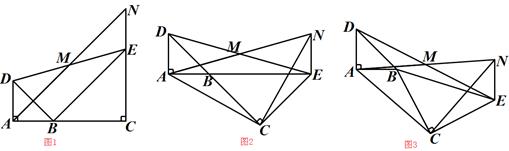
相关知识点
推荐套卷
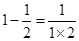 ;②
;② ;
;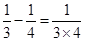 ;④
;④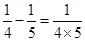 ;
;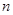 个算式:;
个算式:; .
.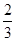 表示成不同的单位分数的和的形式.(写出一种即可)
表示成不同的单位分数的和的形式.(写出一种即可)

 ()=
()=


 只有一个整数解。
只有一个整数解。 -
- )÷
)÷ ,其中x=1
,其中x=1 粤公网安备 44130202000953号
粤公网安备 44130202000953号