辨析纠错.
已知:如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.
求证:四边形AEDF是菱形.对于这道题,
小明是这样证明的.
证明:∵AD平分∠BAC,∴∠1=∠2(角平分线的定义).
∵DE∥AC,∴∠2=∠3(两直线平行,内错角相等).
∴∠1=∠3(等量代换).
∴AE=DE(等角对等边).同理可证:AF=DF.
∴ 四边形AEDF是菱形(菱形定义).
老师说小明的证明过程有错误,你能看出来吗?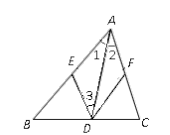
(1)请你帮小明指出他错在哪里.
(2)请你帮小明做出正确的解答.
相关知识点
推荐套卷
 .有酒后开车;
.有酒后开车; .喝酒后不开车或请专业司机代驾;
.喝酒后不开车或请专业司机代驾; .开 车当天不喝酒;
.开 车当天不喝酒; .从不喝酒.将这次调查情况整理并绘制了如下尚不完整的统计图一和图二,请根据相关信息,解答下列问题.
.从不喝酒.将这次调查情况整理并绘制了如下尚不完整的统计图一和图二,请根据相关信息,解答下列问题.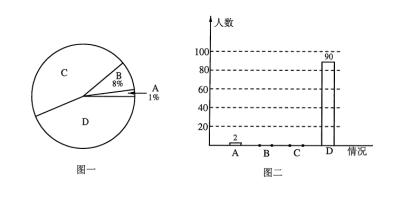
 、
、 分别在线段
分别在线段 、
、 上,
上, .
.
 ∽△
∽△ ;
; ,
, ,
, ,求
,求 .
. .
. ). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.
). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.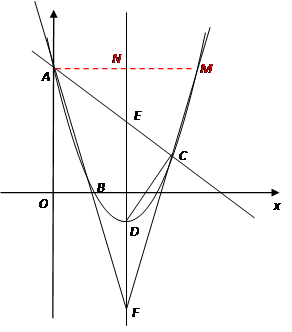
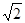 ,求 正方形ABCD的面积.
,求 正方形ABCD的面积.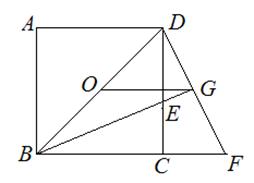
 粤公网安备 44130202000953号
粤公网安备 44130202000953号