小华骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校．以下是他本次上学所用的时间与离家距离的关系示意图．根据图中提供的信息回答下列问题：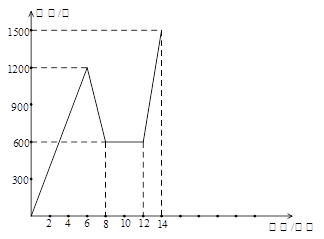
（1）小华家到学校的路程是多少米？
（2）在整个上学的途中哪个时间段小华骑车速度最快，最快的速度是多少米/分？
（3）小华在书店停留了多少分钟？
（4）本次上学途中，小华一共行驶了多少米？
（5）如果小华到校后立刻以300米/分的匀速度回家，请在原图上画出小华回家所用时间与离家距离的关系图象．
相关试题
阅读材料：如果
、
是一元二次方程
(
≠0)的两根，那么，＋＝
，
＝
．这就是著名的韦达定理．
现在我们利用韦达定理解决问题：
已知
与
是方程
的两根，
（1）填空：＋＝________；
＝________；
（2）计算
的值．
，
，
.
，
，求下列各式的值：
；
.
，两车之间的距离为
，图中的折线表示
与
之间的函数关系．
相关知识点
推荐套卷
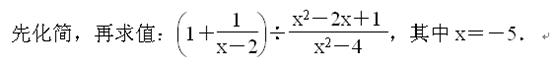
粤公网安备 44130202000953号