七巧板游戏是将一个正方形分割成七块,然后用这七块拼接成丰富多彩的几何图形.如图(a)是正方形的一种分割方法,并在每块上标了号码.
(1)设正方形网格的边长为1,则面积为2的有 号图形;
(2)只改变图(a)中的7号图形的位置,使它和其他部分拼成一个新的多边形,请在图(b)中画出所拼的图形(只需画出7号图形);
(3)将这副七巧板的七块图形重新拼成一个和图(a)、图(b)形状不同的多边形,(不留缝隙且不相互重叠),请在图(c)中画出所拼的图形,并使多边形的顶点落在格点上.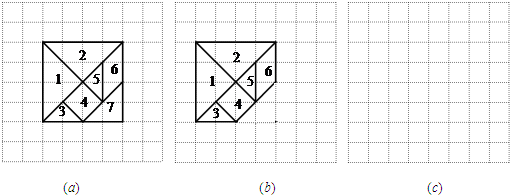
相关知识点
推荐套卷

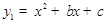 的图象与x轴交于A、B 两点,与
的图象与x轴交于A、B 两点,与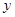 轴交于点C,且点B的坐标为(1,0),点C的坐标为
轴交于点C,且点B的坐标为(1,0),点C的坐标为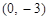 ,一次函数
,一次函数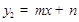 的图象过点A、C.
的图象过点A、C.
 时,
时,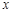 的取值范围.
的取值范围. 的图象与反比例函数
的图象与反比例函数 的图象的一个交点为A(1,m),点B(n,1)在反比例函数的图象上.
的图象的一个交点为A(1,m),点B(n,1)在反比例函数的图象上.
 轴上一点,且满足△POB的面积为6,求P点的坐标.
轴上一点,且满足△POB的面积为6,求P点的坐标.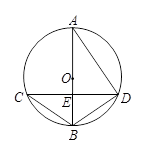
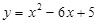 .
. 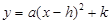 的形式;
的形式; 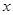 取何值时,
取何值时,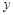 随
随 粤公网安备 44130202000953号
粤公网安备 44130202000953号