(本小题12分)已知□ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF.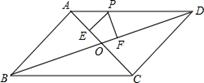
(1)如图,若PE=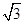 ,EO=1,求∠EPF的度数;
,EO=1,求∠EPF的度数;
(2)若点P是AD的中点,点F是DO的中点,BF=BC+3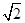 -4,求BC的长.
-4,求BC的长.
相关知识点
推荐套卷
(本小题12分)已知□ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF.
(1)如图,若PE=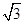 ,EO=1,求∠EPF的度数;
,EO=1,求∠EPF的度数;
(2)若点P是AD的中点,点F是DO的中点,BF=BC+3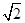 -4,求BC的长.
-4,求BC的长.