某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校旗杆的高,小明站在点B处测得旗杆顶端E点的仰角为45°,小军站在点D处测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF.(结果精确到0.1米,参考数据: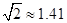 ,
,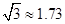 )
)
某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校旗杆的高,小明站在点B处测得旗杆顶端E点的仰角为45°,小军站在点D处测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF.(结果精确到0.1米,参考数据: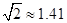 ,
,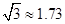 )
)