下表给出了代数式 与
与 的一些对应值:
的一些对应值:
| x |
… |
0 |
1 |
2 |
3 |
4 |
… |
 +bx+c +bx+c |
… |
3 |
|
-1 |
|
3 |
… |
(1)请在表内的空格中填入适当的数;
(2)设y= +bx+c,则当x取何值时,y>0?
+bx+c,则当x取何值时,y>0?
(3)请说明经过怎样平移函数y= +bx+c的图象得到函数y=
+bx+c的图象得到函数y= +1的图象
+1的图象
相关知识点
推荐套卷
 -1=
-1= ,求:
,求: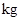 ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率. 粤公网安备 44130202000953号
粤公网安备 44130202000953号