如图,O为坐标原点,点F为抛物线C1: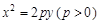 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2: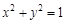 相切于点Q.
相切于点Q.
(Ⅰ)当直线PQ的方程为 时,求 抛物线C1的方程;
时,求 抛物线C1的方程;
(Ⅱ)当正数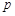 变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求
变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求 的最小值.
的最小值.
相关知识点
推荐套卷
如图,O为坐标原点,点F为抛物线C1: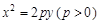 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2: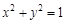 相切于点Q.
相切于点Q.
(Ⅰ)当直线PQ的方程为 时,求 抛物线C1的方程;
时,求 抛物线C1的方程;
(Ⅱ)当正数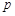 变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求
变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求 的最小值.
的最小值.