为了测量校园内一棵大树的高度，学校数学应用实践小组做了如下的

首页 / 初中数学 / 试题详细

更新 2022-09-03
科目数学
题型解答题
难度中等
浏览 1778

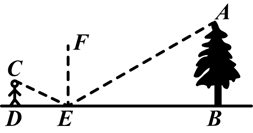
为了测量校园内一棵大树的高度，学校数学应用实践小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计了如图的测量方案，把镜子放在离树(AB)8.7m的点E处，然后沿直线BE后退到点D，这时恰好在镜子里看到树顶点A，再用皮尺测量得DE＝2.7m，观察者眼睛距地面的高CD＝1.6m，请你计算树(AB)的高度．(精确到0.1m)

登录免费查看答案和解析

相关试题

在一条笔直的滑道上有黑、白两个小球同向运动，黑球在 $A$ 处开始减速，此时白球在黑球前面 $70 c m$ 处．

小聪测量黑球减速后的运动速度 $v$ （单位： $c m / s$ ）、运动距离 $y$ （单位： $c m$ ）随运动时间 $t$ （单位： $s$ ）变化的数据，整理得下表．

运动时间t/s	$0$	$1$	$2$	$3$	$4$
运动速度v/cm/s	$10$	$9.5$	9	$8.5$	$8$
运动距离y/cm	$0$	$9.75$	19	$27.75$	$36$

小聪探究发现，黑球的运动速度 $v$ 与运动时间 $t$ 之间成一次函数关系，运动距离 $y$ 与运动时间 $t$ 之间成二次函数关系．

（1）直接写出 $v$ 关于 $t$ 的函数解析式和 $y$ 关于 $t$ 的函数解析式（不要求写出自变量的取值范围）；

（2）当黑球减速后运动距离为 $64 c m$ 时，求它此时的运动速度；

（3）若白球一直以 $2 c m / s$ 的速度匀速运动，问黑球在运动过程中会不会碰到白球？请说明理由．

题型：未知
难度：未知

收藏答案/解析

如图，以 $A B$ 为直径的 $⊙ O$ 经过 $△ A B C$ 的顶点 $C$ ， $A E ， B E$ 分别平分 $∠ B A C$ 和 $∠ A B C$ ， $A E$ 的延长线交 $⊙ O$ 于点 $D$ ，连接 $B D$ ．

（1）判断 $△ B D E$ 的形状，并证明你的结论；

（2）若 $A B ＝ 10$ ， $B E ＝ 2 \sqrt{10}$ ，求 $B C$ 的长．

题型：未知
难度：未知

收藏答案/解析

为庆祝中国共青团成立 $100$ 周年，某校开展四项活动： $A$ 项参观学习， $B$ 项团史宣讲， $C$ 项经典诵读， $D$ 项文学创作，要求每名学生在规定时间内必须且只能参加其中一项活动．该校从全体学生中随机抽取部分学生，调查他们参加活动的意向，将收集的数据整理后，绘制成如下两幅不完整的统计图．