七年级我们学过三角形的相关知识,在动手实践的过程中,发现了一个基本事实:
三角形的三条高(或三条高所在直线)相交于一点.
其实,有很多八年级、九年级的问题均可用此结论解决.
【运用】如图,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.
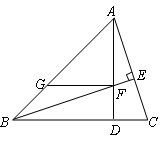
小方同学在解答此题时,利用了上述结论,她的方法如下:
连接CF并延长,交AB于点M,
∵△ABC的高AD与高BE相交于点F,
∴CM为△ABC的高.
(请你在下面的空白处完成小方的证明过程.)
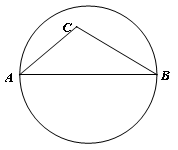
【操作】如图AB是圆的直径,点C在圆内,请仅用无刻度的直尺画出△ABC中AB边上的高.