如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连结BE交AC于点F,连结DF.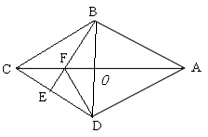
(1)证明:△CBF≌△CDF;
(2)若AC=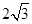 ,BD=2,求四边形ABCD的周长;
,BD=2,求四边形ABCD的周长;
(3)请你添加一个条件,使得∠EFD=∠BAD,并予以证明.
相关知识点
推荐套卷
如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连结BE交AC于点F,连结DF.
(1)证明:△CBF≌△CDF;
(2)若AC=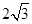 ,BD=2,求四边形ABCD的周长;
,BD=2,求四边形ABCD的周长;
(3)请你添加一个条件,使得∠EFD=∠BAD,并予以证明.