(本题满分为15分)如图，焦点在
轴的椭圆，离心率
，且过点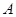
（-2，1），由椭圆上异于点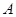的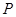
点发出的光线射到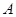点处被直线
反射后交椭圆于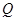
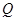点(点与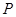点不重合)．
（1）求椭圆标准方程；
（2）求证:直线
的斜率为定值；
（3）求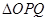
的面积的最大值．
到定点
的距离与它到直线
的距离之比为常数
，求点
的轨迹。
，长轴长为
，在椭圆上有一点
到左准线的距离为
，求点
为抛物线
上位于
轴两侧的两点。（1）若
，证明直线
恒过一个定点；（2）若
，
为钝角，求直线
求抛物线
上的点到
点的距离的最小值。
的焦点
作一直线，和抛物线相交于
，求
的长。推荐套卷
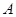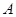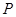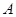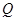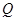(本题满分为15分)如图，焦点在轴的椭圆，离心率，且过点（-2，1），由椭圆上异于点的点发出的光线射到点处被直线反射后交椭圆于点(点与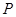点不重合)．
（1）求椭圆标准方程；
（2）求证:直线的斜率为定值；
（3）求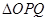的面积的最大值．
粤公网安备 44130202000953号