如图1，在△ACB和△AED中，AC=BC，AE=DE，∠ACB＝∠AED＝90°，点E在AB上，点D在AC上．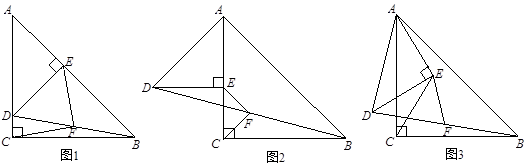
（1）若F是BD的中点，求证：CF=EF；
（2）将图1中的△AED绕点A顺时针旋转，使AE恰好在AC上（如图2）．若F为BD上一点，且CF=EF，求证：BF= DF；
（3）将图1中的△AED绕点A顺时针旋转任意的角度（如图3）．若F是BD的中点．探究CE与EF的数量关系，并证明你的结论．
相关试题
A、B两家公司都准备向社会招聘人才，两家公司条件基本相同，只有工资待遇有如下差异：
A公司年薪两万元，每年加工龄工资400元，
B公司半年薪一万元，每半年加工龄工资100元，
求A、B两家公司第n年的年薪分别是多少，从经济角度考虑，选择哪家公司有利？
推荐套卷
粤公网安备 44130202000953号