如图,已知二次函数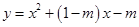 (其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC.
(其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC. 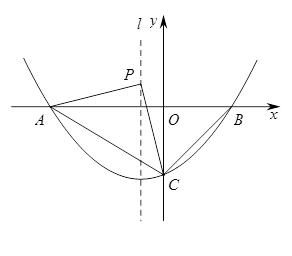
(1)∠ABC的度数为 °;
(2)求P点坐标(用含m的代数式表示);
(3)在坐标轴上是否存在点Q(与原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由.
相关知识点
推荐套卷
如图,已知二次函数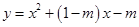 (其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC.
(其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC. 
(1)∠ABC的度数为 °;
(2)求P点坐标(用含m的代数式表示);
(3)在坐标轴上是否存在点Q(与原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由.