如图,曲线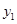 抛物线的一部分,且表达式为:
抛物线的一部分,且表达式为: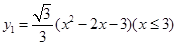 曲线
曲线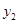 与曲线
与曲线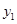 关于直线
关于直线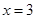 对称。
对称。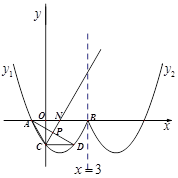
(1)求A、B、C三点的坐标和曲线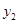 的表达式;
的表达式;
(2)过点D作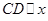 轴交曲线
轴交曲线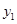 于点D,连接AD,在曲线
于点D,连接AD,在曲线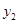 上有一点M,使得四边形ACDM为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标。
上有一点M,使得四边形ACDM为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点M的横坐标。
(3)设直线CM与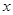 轴交于点N,试问在线段MN下方的曲线
轴交于点N,试问在线段MN下方的曲线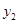 上是否存在一点P,使△PMN的面积最大?若存在,求出点P的坐标;若不存在,请说明理由。
上是否存在一点P,使△PMN的面积最大?若存在,求出点P的坐标;若不存在,请说明理由。
相关知识点
推荐套卷
 地往北60m的
地往北60m的 处有一幢民房,西80m的
处有一幢民房,西80m的 处有一变电设施,在
处有一变电设施,在 的中点
的中点 处有一古建筑.因施工需要必须在
处有一古建筑.因施工需要必须在
 的半圆
的半圆 ,过直径
,过直径 上一点
上一点 ,作
,作 交半圆于点
交半圆于点 ,且
,且 ,试求
,试求 的长.
的长.
 (如图),试取斜边
(如图),试取斜边 上的一点为圆心画图,使点
上的一点为圆心画图,使点 ,
, ,
, 分别在所画的圆内、圆外和圆上.
分别在所画的圆内、圆外和圆上.
 ,连结
,连结 ,
, 相交于点
相交于点 ,以点
,以点 为圆心,
为圆心, cm长为半径画圆,试判断点
cm长为半径画圆,试判断点 ,
, ,
, ,
,
 粤公网安备 44130202000953号
粤公网安备 44130202000953号