如图，在Rt△ABC中，∠C=90°．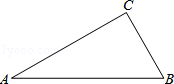
（1）根据要求用尺规作图：过点C作斜边AB边上的高CD，垂足为D（不写作法，只保留作图痕迹）；
（2）在（1）的条件下，请写出图中所有与△ABC相似的三角形．
．
．
m+n的值．相关知识点
推荐套卷
如图，在Rt△ABC中，∠C=90°．
（1）根据要求用尺规作图：过点C作斜边AB边上的高CD，垂足为D（不写作法，只保留作图痕迹）；
（2）在（1）的条件下，请写出图中所有与△ABC相似的三角形．
粤公网安备 44130202000953号