（本小题满分8分）已知：正方形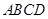
中，∠MAN=45°，∠MAN绕点
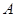顺时针旋转，它的两边分别交
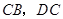（或它们的延长线）于点
．
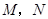当∠MAN绕点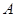旋转到BM=DN时（如图1），易证BM+DN=MN．
（1）当∠MAN绕点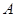旋转到BM≠DN时（如图2），线段
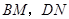和
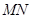之间有怎样的数量关系？写出猜想，并加以证明．
（2）当∠MAN绕点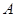旋转到如图3的位置时，线段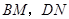和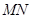之间又有怎样的数量关系？请直接写出你的猜想．
cos60°+sin45°•tan30°．
．求△BCD的面积．
﹣6
﹣tan60°．
cos45°﹣（
）2+（2﹣tan45°）0；
．相关知识点
推荐套卷
（本小题满分8分）已知：正方形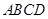中，∠MAN=45°，∠MAN绕点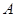顺时针旋转，它的两边分别交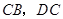（或它们的延长线）于点．
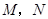当∠MAN绕点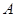旋转到BM=DN时（如图1），易证BM+DN=MN．
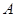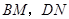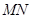（1）当∠MAN绕点旋转到BM≠DN时（如图2），线段和之间有怎样的数量关系？写出猜想，并加以证明．
（2）当∠MAN绕点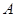旋转到如图3的位置时，线段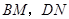和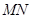之间又有怎样的数量关系？请直接写出你的猜想．
粤公网安备 44130202000953号