如图,已知等腰△AOB放置在平面直角坐标系xOy中, OA=OB,点B的坐标为(3,4).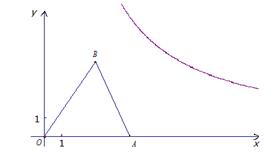
(1)求直线AB的解析式;
(2)问将等腰△AOB沿x轴正方向平移多少个单位,能使点B落在反比例函数 (x>0)的图象上.
(x>0)的图象上.
相关知识点
推荐套卷
如图,已知等腰△AOB放置在平面直角坐标系xOy中, OA=OB,点B的坐标为(3,4).
(1)求直线AB的解析式;
(2)问将等腰△AOB沿x轴正方向平移多少个单位,能使点B落在反比例函数 (x>0)的图象上.
(x>0)的图象上.