如图1,抛物线 经过(4,0),
经过(4,0),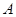
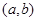 是抛物线上的任意一点,直线
是抛物线上的任意一点,直线 经过
经过 且与
且与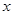 轴平行,过
轴平行,过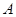 作
作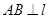 于
于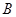 点.
点.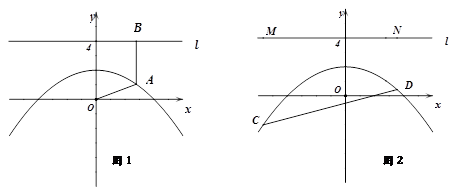
(1)直接写出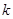 的值:
的值: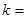 ;
;
(2)当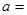 0时,
0时, ,
,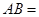 ;
;
当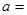 8时,
8时, ,
,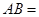 ;
;
(3)由(2)的结论,请你猜想:对于抛物线上的任意一点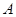 ,
, 与
与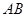 有怎样的大小关系,并证明你的猜想.
有怎样的大小关系,并证明你的猜想.
(4) 如图2,已知线段 12,线段的两端点
12,线段的两端点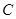 、
、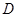 在抛物线上滑动,求
在抛物线上滑动,求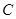 、
、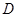 两点到直线
两点到直线 的距离之和的最小值.
的距离之和的最小值.
相关知识点
推荐套卷
如图1,抛物线 经过(4,0),
经过(4,0),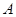
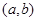 是抛物线上的任意一点,直线
是抛物线上的任意一点,直线 经过
经过 且与
且与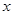 轴平行,过
轴平行,过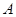 作
作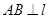 于
于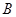 点.
点.
(1)直接写出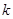 的值:
的值: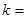 ;
;
(2)当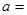 0时,
0时, ,
,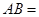 ;
;
当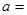 8时,
8时, ,
,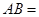 ;
;
(3)由(2)的结论,请你猜想:对于抛物线上的任意一点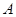 ,
, 与
与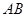 有怎样的大小关系,并证明你的猜想.
有怎样的大小关系,并证明你的猜想.
(4) 如图2,已知线段 12,线段的两端点
12,线段的两端点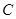 、
、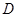 在抛物线上滑动,求
在抛物线上滑动,求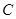 、
、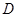 两点到直线
两点到直线 的距离之和的最小值.
的距离之和的最小值.