在“不闯红灯,珍惜生命”活动中,东方中学的关欣和李好两位同学某天来到城区中心的十字
路口,观察、统计上午7:00-12:00中闯红灯的人次,制作了如下的两个数据统计图: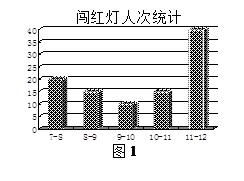

(1)求图1中提供的五个数据(各时段闯红灯人次)的众数、中位数和平均数。
(2)估计一个月(按30天计算)上午7:00-12:00在该路口闯红灯的未成年人约有______人次。
(3)请你根据统计图提供的信息向交通管理部门提出一条合理化建议。
相关知识点
推荐套卷
在“不闯红灯,珍惜生命”活动中,东方中学的关欣和李好两位同学某天来到城区中心的十字
路口,观察、统计上午7:00-12:00中闯红灯的人次,制作了如下的两个数据统计图: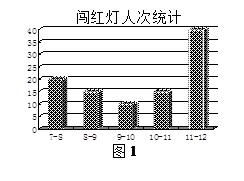

(1)求图1中提供的五个数据(各时段闯红灯人次)的众数、中位数和平均数。
(2)估计一个月(按30天计算)上午7:00-12:00在该路口闯红灯的未成年人约有______人次。
(3)请你根据统计图提供的信息向交通管理部门提出一条合理化建议。